ルンゲクッタ

f:id:hope_is_dream:20161211170440p:plain

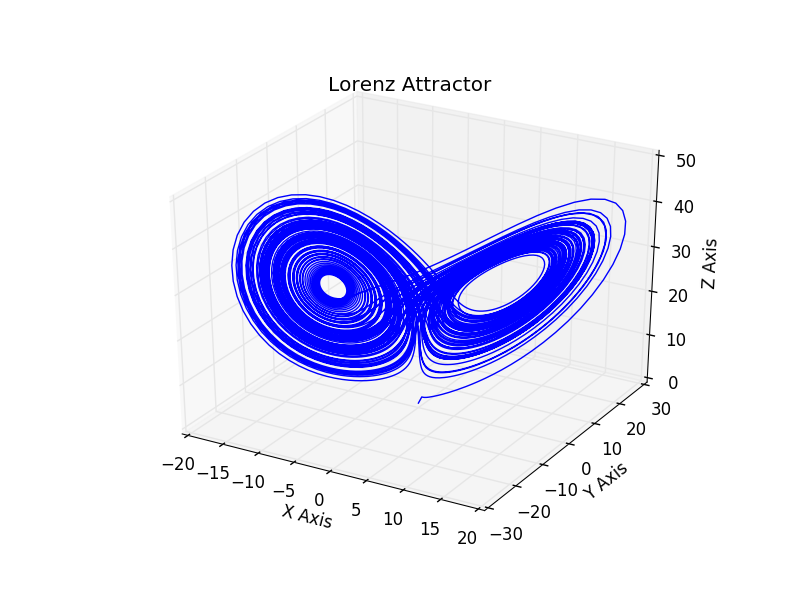
最近ドリフトのシミュレータを書いている。シミュレーションにあたって車両の運動を、適当な車両運動モデルを作って時間発展を計算させている。さて、最近つくった私の貧弱モデルをオイラー法で動かすと、どうも数値振動しているのか車体が「グラグラ」して気持ち悪い。運動方程式の立て方も悪いので一概に原因が分からない。方程式の立て方で復元力によって振動しているかもしれないし、数値微分の振動かもしれない。と。原因はいろいろ考えられるわけだ。原因は一つ一つつぶしていくのがセオリーなので、ひとまずオイラー法を精度の良いルンゲクッタ法に置き換える。(オイラー法では車両が上手く動かせないことは以前に確認済み)。今回は車両の回転方程式と並進の2方程式を解く。変数は重心の横滑り角度と、角速度の二つなので、れんせい方程式のルンゲクッタを計算する練習で、ローレンツ・アトラクターをお題としてベースのコードを書く。

まぁ、こちらの記事をpythonで書き直しただけでございます。ルンゲクッタ法で様々な連立微分方程式を解く数値計算例(C言語)

まずはそのまま書き下したコード

# -*- coding:utf-8 -*-
"""
runge kutta

http://www.geocities.jp/supermisosan/rksimultaneousequation.html


:Equation:
dxdt = 10*(y-x)             --- (1)
dydt = 28*x - y - x*z       --- (2)
dzdt = -(8./3.)*z + x*y     --- (3)

"""
import numpy as np

def f1(t,x,y,z):
    return 10.*(y - x)

def f2(t,x,y,z):
    return  (28.*x) - y - (x*z) 

def f3(t,x,y,z):
    return  (-8./3.)*z + (x*y) 


def main():
    # time step
    dt = 0.01
    tmax = dt * 10000
    # initial condition
    t = 0.0
    x = 0.
    y = 1.
    z = 1.05

    k0=[0,0,0]
    k1=[0,0,0]
    k2=[0,0,0]
    k3=[0,0,0]

    write(["t","x","y","z"], header=True)

    while t<=tmax:

        k0[0]= dt * f1(t,x,y,z);
        k0[1]= dt * f2(t,x,y,z);
        k0[2]= dt * f3(t,x,y,z);

        k1[0]= dt * f1(t+dt/2.0, x+k0[0]/2.0, y+k0[1]/2.0, z+k0[2]/2.0);
        k1[1]= dt * f2(t+dt/2.0, x+k0[0]/2.0, y+k0[1]/2.0, z+k0[2]/2.0);
        k1[2]= dt * f3(t+dt/2.0, x+k0[0]/2.0, y+k0[1]/2.0, z+k0[2]/2.0);

        k2[0]= dt * f1(t+dt/2.0, x+k1[0]/2.0, y+k1[1]/2.0, z+k1[2]/2.0);
        k2[1]= dt * f2(t+dt/2.0, x+k1[0]/2.0, y+k1[1]/2.0, z+k1[2]/2.0);
        k2[2]= dt * f3(t+dt/2.0, x+k1[0]/2.0, y+k1[1]/2.0, z+k1[2]/2.0);

        k3[0]= dt * f1(t+dt, x+k2[0], y+k2[1], z+k2[2]);
        k3[1]= dt * f2(t+dt, x+k2[0], y+k2[1], z+k2[2]);
        k3[2]= dt * f3(t+dt, x+k2[0], y+k2[1], z+k2[2]);

        dx = (k0[0]+2.0*k1[0]+2.0*k2[0]+k3[0])/6.0;
        dy = (k0[1]+2.0*k1[1]+2.0*k2[1]+k3[1])/6.0;
        dz = (k0[2]+2.0*k1[2]+2.0*k2[2]+k3[2])/6.0;

        x = x + dx
        y = y + dy
        z = z + dz

        write([t,x,y,z])
        print(t,x,y,z, k0,k1,k2,k3)
        t = t + dt

def post(filename="lorenz.csv"):
    import numpy as np
    import matplotlib.pyplot as plt
    from mpl_toolkits.mplot3d import Axes3D

    data = np.genfromtxt("lorenz.csv", delimiter="," ,filling_values=(0, 0, 0, 0))
    ts = data[:,0]
    xs = data[:,1]
    ys = data[:,2]
    zs = data[:,3]

    fig = plt.figure()
    ax = fig.gca(projection='3d')

    ax.plot(xs, ys, zs)
    ax.set_xlabel("X Axis")
    ax.set_ylabel("Y Axis")
    ax.set_zlabel("Z Axis")
    ax.set_title("Lorenz Attractor")

    plt.show()

def write(line, header=False):

    import csv

    # Header
    if header:
        with open('lorenz.csv', 'w') as f:
            writer = csv.writer(f, lineterminator='\n') # 改行コード（\n）を指定しておく
            writer.writerow(line)     # list（1次元配列）の場合
    # Body
    if header == False:
        with open('lorenz.csv', 'a') as f:
            writer = csv.writer(f, lineterminator='\n') # 改行コード（\n）を指定しておく
            writer.writerow(line)     # list（1次元配列）の場合
if __name__ == '__main__':
    main()
    post()

そして、さらに省略できたコード

mplot3d example code: lorenz_attractor.py — Matplotlib 1.5.3 documentation

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


def lorenz(x, y, z, s=10, r=28, b=2.667):
    x_dot = s*(y - x)
    y_dot = r*x - y - x*z
    z_dot = x*y - b*z
    return np.array([x_dot, y_dot, z_dot])


t=0
dt = 0.01
stepCnt = 10000

# Need one more for the initial values
xs = np.empty((stepCnt + 1,))
ys = np.empty((stepCnt + 1,))
zs = np.empty((stepCnt + 1,))

# Setting initial values
xs[0], ys[0], zs[0] = (0., 1., 1.05)
k0=[0,0,0]
k1=[0,0,0]
k2=[0,0,0]
k3=[0,0,0]

# Stepping through "time".
for i in range(stepCnt):
    x,y,z=xs[i],ys[i],zs[i]

    k0 = dt * lorenz(x,y,z)
    k1 = dt * lorenz(x+k0[0]/2., y+k0[1]/2., z+k0[2]/2.)
    k2 = dt * lorenz(x+k1[0]/2., y+k1[1]/2., z+k1[2]/2.)
    k3 = dt * lorenz(x+k2[0], y+k2[1], z+k2[2])

    dx = (k0[0]+2.0*k1[0]+2.0*k2[0]+k3[0])/6.0
    dy = (k0[1]+2.0*k1[1]+2.0*k2[1]+k3[1])/6.0
    dz = (k0[2]+2.0*k1[2]+2.0*k2[2]+k3[2])/6.0

    xs[i+1] = xs[i] + dx
    ys[i+1] = ys[i] + dy
    zs[i+1] = zs[i] + dz


fig = plt.figure()
ax = fig.gca(projection='3d')

ax.plot(xs, ys, zs)
ax.set_xlabel("X Axis")
ax.set_ylabel("Y Axis")
ax.set_zlabel("Z Axis")
ax.set_title("Lorenz Attractor")

plt.show()